Core Plus Mathematics Course 2 Teacher's Edition Pdf

Core-Plus Mathematics: chapter by chapter

If you are a high-school student and have a misfortune of using the Core-Plus Mathematics course, you know that fishing out the few bits of algebra, geometry, physics, and statistics buried deep inside these books is a dirty and thankless job.

Core-Plus Mathematics Course 1, Unit 1, Lesson 1

I am going to take this unrewarding trek with you, helping y ou to figure out what the authors of the book wanted to teach. I will also add information that should have been in the course, but is sorely missing. Because, let us be frank, Core-Plus Mathematics is not about mathematics — these are fiction books, chapter books, and like any chapter book, the chapters in Core-Plus course have very little relation one to another.

Unlike traditional textbooks that have theoretical material, definitions, examples, maybe some proofs and then exercises to work on, the Core-Plus course is a wall of text. If you are an English Learner you are going to hate this course because it is incomprehensible; if you are native English Speaker you are going to hate this course because it is vague and diluted.

There are four books in the course, one book per high-school year. Each book has two editions: a student's edition and a teacher's edition.

I am going to start from the beginning, with the first book in the series, the Course 1, Student's edition, meant to be used in 9th grade. There are 8 units with about 3 to 4 lessons in each, altogether 28 lessons. Considering that a typical school year lasts 36 weeks, I would say that the intended pacing is one lesson per week, allowing extra time for incidentals like high stake testing, which can easily take a week off your regular schedule.

Unit 1: Patterns of Change

The first unit is called Patterns of Change. This is the narrative that the book tries to build, where every chapter studies some sort of a pattern. This is not a strike against the course and could be a valid approach; in fact, Godfrey Harold Hardy, a British mathematician, wrote:

A mathematician, like a painter or a poet, is a maker of patterns.

Lesson 1: Cause and Effect

The first lesson tells a mildly amusing story about throwing people off a bridge with their feet tied with a stretchy cord. It also suggests making money from this enterprise. Before you jump into bungee jumping business you need to make sure, first, that you don't kill your customers and second, that you will earn enough money. If this does not work, you can try making money by throwing dice or coins and betting on certain combinations. If you have failed here too, then you can resort to watching car racing, trying to figure out when the race ends.

Linear function and Hooke's Law

Let us start with bungee jumping first. The single biggest physics idea about throwing people off a bridge with their legs tied up is that a rubber cord becomes longer when you try to stretch it. You may scoff at this idea as self-evident, but if instead of a rubber band you used a steel chain, it would not stretch, ripping off jumper's limbs. Therefore, some materials are stretchy or squishy — the technical term is "elastic" — and other materials are not.

Elasticity is the tendency of solid materials to return to their original shape after forces applied on them are removed.

Another takeaway is that the more force you apply to a stretchy material, the more it stretches. Naturally, one wonders: is it possible to figure out how much a particular material stretches depending on how much force is applied?

The textbook prudently suggests experimenting in a school lab first instead of testing on live customers. The book does not stop to ponder why you can apply the results of a test, conducted in a laboratory with a small piece of rubber band, to real-life bungee jumping business. A missed teaching opportunity, one out of many.

Core-Plus Mathematics, Course 1, Lesson 1

Instead, the textbook focuses on teamwork, where some members of a team will do the experiments, other will record it, yet other will verify the correctness of the data. Teamwork is a useful work pattern considering that most manufacturing jobs have moved to the Far East, so what was formerly a one-man job now should be done as a team.

In case you fail to figure out the relationship between the force, applied to a rubber band, and its length, the book provides a formula that imaginary girls from an imaginary school in the presumably real state of Iowa came up with: L=30+20×W, where L is the length of the rubber band, w is the weight in ounces, and 30 is the length of the rubber band without weight attached to it, that is, in its un-stretched condition.

The textbook does not mention Robert Hooke, an English natural philosopher, who experimented with metal springs about 350 years ago and came up with a "law" for elastic deformation. This "law" is empirical, that is, is based on experimental data, and as such, works only within certain constraints.

The Hooke's Law can be written as F=k×x, where x is the change in length, F is the force, and k is the positive number, a characteristic of the material.

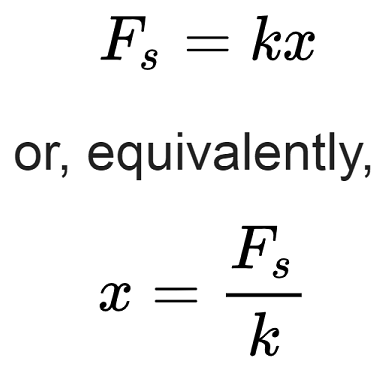
So, assuming that you came up with a formula L=20+0.15×w for the total length of the rubber band depending on weight attached to its end, how can you apply it to bungee jumping business? The book only cursory touches on this topic in the Review section, paragraph 14, which asks: considering that the extended length of the bungee cord is different depending on customer's weight, should the operator of the "bungee apparatus" change the jump-off height for each person? Why or why not?

Well, the whole point of jumping off a bridge with the legs tied is to have safe yet scary experience, when you think you are going to die, but you don't. Meaning, that the extended length of the cord must be such that the jumper almost hits the ground. Considering that changing jump-off point is usually not feasible, what do you do? Well, you change the slack-off, the length of the cord in the un-stretched condition. In the formula this is a constant number 20 added to the product of customer's weight and an elasticity coefficient. So, for real-life situation, we want to make total length a constant, and instead to calculate and adjust the slack-off for each customer. Say, the height is 50 m, and you want 5 m safety margin, then you want L to be 45 m, so: 45=S+0.15×w, from which we can get S=45–0.15×W. The book completely misses this important observation.

Quadratic function and ticket price optimization

Now it is time to make money off your bungee business. How much to charge for a ticket, this is a million dollar question. First of all, let us figure out how much money will we make, if we know ticket price and the number of tickets sold: we multiply one onto another: M=p×N, where M is the amount of money we make, p is the ticket price, and N is the number of customers.

But how much to charge per ticket? We want to maximize the p×N product. If we charge too much, few people will turn up. If we charge too little, then the ticket price may not cover the expenses. The textbook suggests using N=50-p rule for figuring out how many tickets could be sold: if price is zero, that is, the jumps are free, then 50 people will show up (not everyone wants to jump off a bridge with their legs tied up even for free). If you charge $50 per ticket, no one will show up. Substituting 50-p for N in the first formula, the resulting formula is M=(50 -p)×p or M =-p²+50p — it is a quadratic formula.

The authors of the textbook apparently think that the exponent can scare the bejeezus out of students, so they never show the quadratic formula. But how do you find the maximum of a quadratic function? You can use derivative: M'=-2p+50, so for M'=0 you will get 2p=50 or p=25, but this is pre-calculus stuff. You can also find where the function turns to zero — at p=0 and p=50 — and then find a midpoint of this segment, p=25. Because the quadratic function is symmetrical, and because the coefficient at p² is negative, this particular function opens down, so the midpoint would be the maximum.

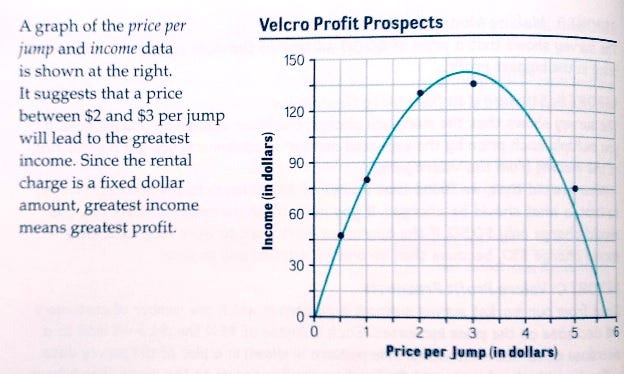
Nah. The book does not do any of that, instead — you guessed it! — it suggests to try several ticket prices, then calculate the total profit, and then, basically, eye it. This is elementary school approach, not a high school math. One may wonder why the book brings up quadratic function so early in the course without saying anything sensible about it.

Concept of probability: getting rich by throwing dice

A third topic in the first Lesson introduces some ideas from probability theory and statistics, but does it in a very clumsy fashion, and confuses the matters. The textbook suggests throwing coins or dice several times, writing the results in the table, then assigning monetary value for every win or loose, and charting a cumulative win-lose graph. No terms like "independent event" or "outcome" are introduced. No distinction is made between theoretical possibility of a particular combination (used in probability theory) and assessing the results of actual tests (this is what statistics deals with). There is no math in this chapter, so you can safely skip it.

Reciprocal function: waiting for a NASCAR race to finish

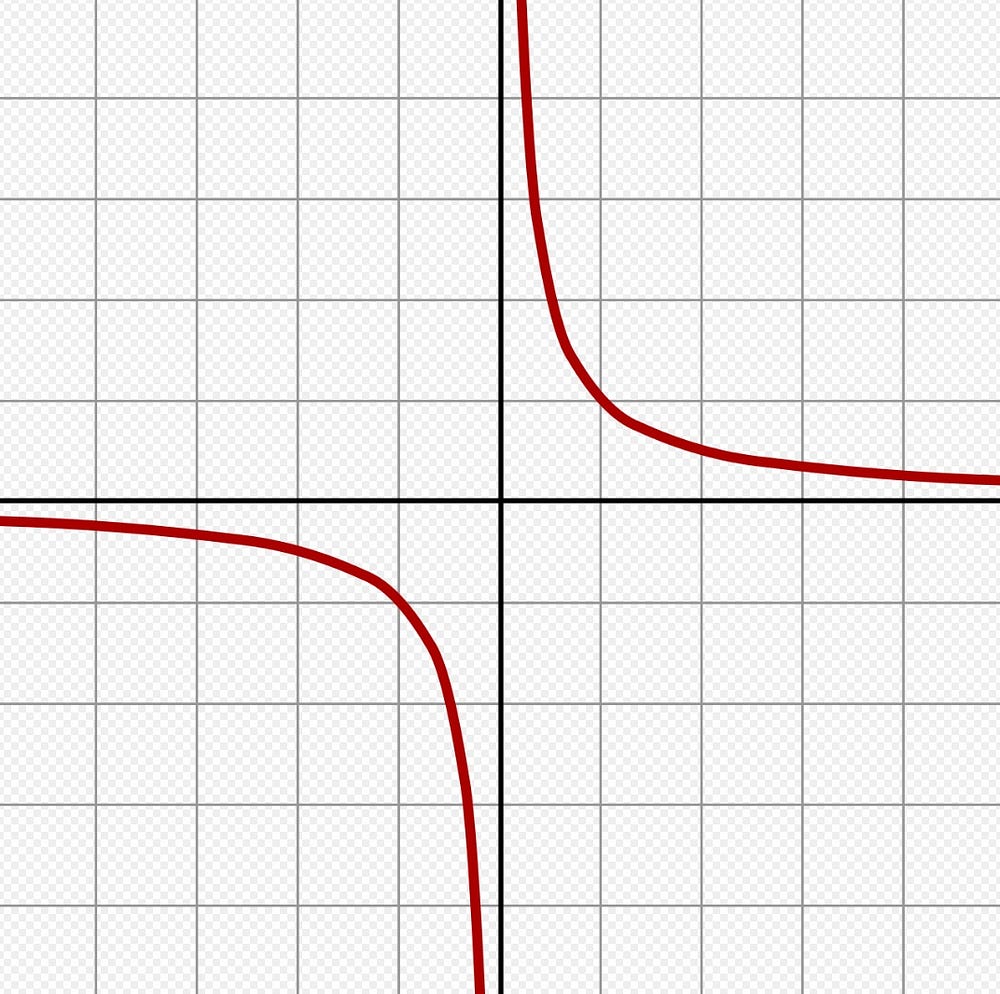
The third investigation introduces the concept of reciprocal function without mentioning the term "reciprocal function" by asking to calculate the time for a car race to finish given winning car's speed and the distance of the race.

A well-known formula for average speed is used: v=s/t, from which you get t=s/v.

In this formula s is the distance of the race, it is a constant, say 500 miles. v is the average speed of a race car, and depending of this speed the time to complete the race varies: the higher the speed, the shorter the time.

The pattern here is the same: calculate some values, put them in a table, then put them onto a Cartesian plane, then maybe connect the points, then look at the graph. Again, there is no math here.

By the end of the first lesson one might think that the main idea of the book seems to be in introduction of several types of relationships — linear, non-linear, reciprocal — without discussing them. At least now you know how the graph or a reciprocal function looks like.

The Law of the Lever

In the Extensions the textbook introduces the concept of the lever. It asks students to figure out the Law of the Lever by looking at the picture. I think it expects too much about analytical skills of the students.

The book does not mention that the the earliest evidence of the lever dates back to the ancient Egypt and Mesopotamia, and that the earliest remaining writings regarding lever are attributed to Archimedes, who exclaimed:

Give me a lever long enough and a fulcrum on which to place it, and I shall move the world!

Coming up in the Lesson 2:

Introduction of exponential relationship without naming it
Introduction of computer spreadsheet apps like Excel
Calculating mean and median without defining what these terms mean.
Sinusoidal function aka sine wave — "Connect the points if it seems to make sense to do so."
An illustration to a classic proof of Pythagorean Theorem without offering the proof itself.